|
GRÁFICO DE
PARETO
Resumo
Um dos
principais objetivos de um programa de qualidade é reduzir perdas
provocadas por itens defeituosos que não atendem às especificações
desejadas. Existem muitos tipos de defeitos que fazem com que um
produto não atenda às especificações. Concentrar esforços no
sentido de eliminar todos os tipos de defeito não é uma política
eficaz, pois geralmente alguns poucos tipos de defeitos são
responsáveis pela maioria das rejeições. É mais eficaz atacar as
causas dos poucos defeitos mais importantes. É exatamente para a
identificação destas causas vitais que podemos utilizar o Gráfico
de Pareto, também conhecido como Diagrama de Pareto. O objetivo
desta monografia é demonstrar as suas principais vantagens e
generalidades.
Introdução
O Gráfico
de Pareto deve seu nome a Vilfredo Pareto (1848 – 1923),
economista italiano do século 19, que foi pioneiro no esforço de
enunciar uma lei de distribuição de rendimentos. Em essência, ele
descobriu que 80% da riqueza estava concentrada em cerca de 20% da
população. O termo se tornou amplamente usado na indústria depois
de sua proeminência nas Mesas Redondas de Gerenciamento conduzidas
na Universidade de Nova Iorque no início da década de 40. Ele
mostra a importância relativa de diferentes causas de um problema,
facilitando a identificação dos aspectos a serem infocados e
solucionados primeiro.
Essa
ferramenta baseia-se no princípio de Pareto, que sugere que um
problema é resultado de um número pequeno de causas. O princípio
de Pareto, também conhecido como regra de 80/20, diz que das
muitas causas de um problema, 80% são trivias e 20% são vitais. Os
triviais representam uma extensa lista de problemas que, apesar de
seu grande número, convertem-se em perdas pouco significativas. Já
os vitais referem-se a um pequeno número de problemas que, embora
pequenos em quantidade, resultam grandes perdas para a empresa.
Daí um dos motivos desta preciosa ferramenta de qualidade auxiliar
o analista a perceber a proporção de cada falha geradora.
Em suma,
o gráfico de Pareto consiste em um gráfico de barras verticais que
disponibiliza a informação de modo que se torne evidente e visual
a priorização dos temas vitais. Tal informação disposta também
permite a implantação de metas numéricas viáveis a serem
atingidas. Por meio deste conhecimento quantitativo determinado, é
possível planejar quais áreas serão trabalhadas para atingir esta
meta estabelecida resolvendo a principal causa do problema de
maneira geral.
Construção do
gráfico
Para se
construir um gráfico de Pareto serão necessários dados
específicos. Antes de se começar a utilizar esta ferramenta é
necessário;
-
que se
determine um problema específico e que seus dados sejam
coletados;
-
alistar as
causas que podem estar provocando o problema;
-
definir uma
medida comum para comparar as causas (categorias) alistadas;
-
estabelecer o
período de tempo em que os daos serão coletados (o ideal é
escolher um período que seja suficiente para representar a
situação, no entanto , nem sempre estudos longos significam
melhores informações);
-
coletar os
dados referente ao problema;
-
distribuir
responsabilidades aos membros da equipe para coletar os dados
necessários.
A partir do
cumprimento destes requisitos será possível a otimização do
gráfico com as suas respectivas classificações e categorias.
Mesmo
sendo uma excelente ferramenta para investigar e melhorar
processos, o gráfico de Pareto tem que ser usado com conhecimento
adequado da estabilidade da característica medida. Se o processo
for estável, o gráfico de Pareto mostra os importantes modos de
falhas ou classificações de problema produzidos pelo sistema de
causas comuns. No entanto se o processo for instável, deve ser
feita uma aprofundada análise dos dados para separar os dados
obtidos quando causas especiais estavam presentes dos dados
produzidos por causas comuns. Deste modo, a análise de Pareto pode
ser feita para as duas situações.
Conclusão
De
fato, o gráfico de Pareto realmente demonstra ser primorozo quando
aplicado à análises e priorização dos aspectos relevantes
relacionados à qualidade de um produto; principalmente quando
empregado em definição de projetos de melhoria e análise de
custos. O fato de tal método evidenciar as principais causas dos
problemas existentes mostra o quanto é usual em qualquer empresa
que tenha por principal meta o progresso e a melhora de qualidade.
Bibliografia
http://
www.estatística.ufrj.br consultado em 22/05/2006
http:// www.unitau.br
consultado em 22/05/2006
http:// wsparis.ws/arqs/sq02.pdf
consultado em 22/05/2006
PROBLEMA:
O aluno apresenta rendimento menor que
os colegas da mesma turma. Para análise do caso foi considerado o
número de horas que o aluno deixa de dedicar às suas obrigações
acadêmicas.
1- LISTA DE VERIFICAÇÃO:
|
PROBLEMAS
LISTADOS |
HORAS/SEMANA |
%
ACUMULADO |
|
deslocamento
para o local |
30 |
44,44 |
|
de curso |
|
|
|
|
|
|
|
obrigações
não acadêmicas |
15 |
66,67 |
|
|
|
|
|
pausa para
alimentação |
10 |
81,48 |
|
|
|
|
|
outros |
10 |
96,30 |
|
|
|
|
|
tempo
despendido em |
2,5 |
100 |
|
lazer |
|
|
|
|
|
|
|
total |
67,5 |
100 |
|
|
|
|
2- GRÁFICO PARETO:
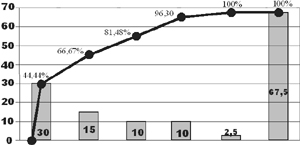
3- DIAGNÓSTICO:
Percebemos através do gráfico que os
itens que mais impedem o aluno de se dedicar às suas obrigações
acadêmicas são “deslocamento para o local de curso” e “obrigações
não acadêmicas”. Juntos estes dois itens chegam a somar 66, 67%
das horas que são desperdiçadas.
4- sugestões para solução
Para que o aluno diminua o tempo
despendido para deslocar-se até o local de curso sugere-se que ele
verifique as rotas e meios usados para o deslocamento. Caso isto
já esteja otimizado, deverá o aluno providenciar moradia mais
próxima ao local do curso. Já para o problema “obrigações não
acadêmicas”, sugere-se que aluno providencie ajuda (família,
Igreja, ONG’s, financeiras e demais instituições) para os
referentes problemas.
|